Ein Machine Learning-Algorithmus generiert mittels Eingabedaten eine Ausgabe. Eine solche Ausgabe könnte beispielsweise die Vorhersage eines Aktienkurses für den nächsten Tag sein. Die Eingabedaten können dabei der Wert des Kurses der vorherigen Tage sein. Aus solchen Eingabedaten wird ein mathematisches Modell erstellt, welches automatisiert Muster in den Daten findet. Diese Muster liefern Einblicke und helfen Entscheidungen oder Vorhersagen zu treffen. Um die Performance solcher Algorithmen zu optimieren, ist Feature Engineering nötig. Ein Feature ist eine messbare Eigenschaft eines Datensatzes, für die zu jeder Observation in den Daten ein Wert existiert. Werden durch Kombination und Transformation von vorhandenen Features neue Features generiert, so wird dies als Feature Engineering bezeichnet. Das Ziel ist es die Daten so zu modifizieren, dass Machine Learning-Algorithmen mehr Muster identifizieren.
Angewandtes Machine Learning ist hauptsächlich Feature Engineering. Es ist schwierig, zeitaufwändig und erfordert Erfahrung sowie Domänenwissen. Durch Analyse, welche Arten von Features am ehesten die Performance eines Algorithmus beeinflussen, kann viel Zeit gespart werden. Kann ein Algorithmus ein Feature selbst erlernen, so besteht keine Notwendigkeit, es bereitzustellen.
Vorherige Analyse von Feature-Engineering-Methoden
In [1] studierte Jeff Heaton gängige Feature-Engineering-Methoden. Er bewertete die Fähigkeit von Machine Learning-Algorithmen, diese Features zu erlernen. Zunächst generierte er gleichmäßig verteilte Zufallszahlen als Eingabe-Features x. Als Nächstes transformierte er ein Feature mit einer bestimmten Methode. Dieses Feature wurde als Label y verwendet. Die Fähigkeit ein Feature selbst zu erlernen wurde dann über die Predictive Performance evaluiert. Die untersuchten Feature-Engineering-Methoden waren:

Heaton testete die Feature-Engineering-Methoden jeweils einzeln. Die Wertebereiche, aus denen er die Eingabe-Features generierte, variierten. Die mittlere quadratische Abweichung (RMSE) ermittelte er jeweils für vier verschiedene Modelle. Dazu gehörten:
- Neuronale Netze
- Support Vector Machines (SVM) mit Gaußschem Kernel
- Random Forests
- Boosted Decision Trees (BDT)
Heaton veröffentlichte die RMSE-Ergebnisse auf seiner GitHub-Seite und kam zu folgenden Schlussfolgerungen:
- Das Verhältnis von Differenzen kann von keinem der Algorithmen selbst erlernt werden.
- Auf Entscheidungsbäumen basierende Algorithmen können Summen nicht erlernen.
- Sowohl das neuronale Netz als auch SVM können Verhältnisse nicht erlernen.
- SVM kann die quadratische Distanz nicht erlernen.
Der RMSE ist jedoch abhängig von den absoluten Werten der Labels und deren Werte variierten über mehrere Größenordnungen zwischen den einzelnen Experimenten. Darüber hinaus folgten die Labels unterschiedlichen Verteilungen. In einigen Fällen kann eine andere Schlussfolgerung gemacht werden, wenn die Eingabe-Features aus einem etwas anderen Wertebereich generiert werden. Daher sind die RMSE-Werte zwischen den verschiedenen Experimenten nicht vergleichbar. Lediglich die RMSE-Werte verschiedener Algorithmen im gleichen Experiment. Um dies zu berücksichtigen, wiederholte ich das Experiment mit einer verbesserten Evaluierungsmethode – dies zeigt einige interessante Unterschiede.
Verbesserte Analyse und Ergebnisse
Ich änderte die Evaluierungsmethode so, dass die Werte der Labels einheitlich und zufällig generiert wurden. Zusätzlich wählte ich den Wertebereich der Labels zwischen 1 und 10. Für alle Experimente wurden dieselben Labels verwendet. Anschließend habe ich die Eingabe-Features mit der inversen Transformation der Labels erstellt. Also anstatt beispielsweise die Labels mit dem Quadrat der Eingabe-Features zu transformieren, habe ich das Eingabe-Feature mit der Quadratwurzel der Labels erstellt.
Falls diese Inversion mehrere Lösungen besitzt, wurde nur eine verwendet. In Experimenten mit mehreren Eingabe-Features habe ich alle bis auf ein Feature zufällig generiert. Die Wertebereiche habe ich so gewählt, dass sich alle Eingabe-Features im gleichen Wertebereich befinden. Außerdem habe ich die Daten für alle Modelle mittels Standardisierung skaliert. Schließlich habe ich für das Neuronale Netz und den BDT unterschiedliche Lernraten ausprobiert. Die Lernrate, mit der das jeweilige Modell am besten performte, wurde verwendet. Das restliche Setup habe ich von Heatons Analyse übernommen. Die Ergebnisse sind in Abbildung 1 dargestellt.
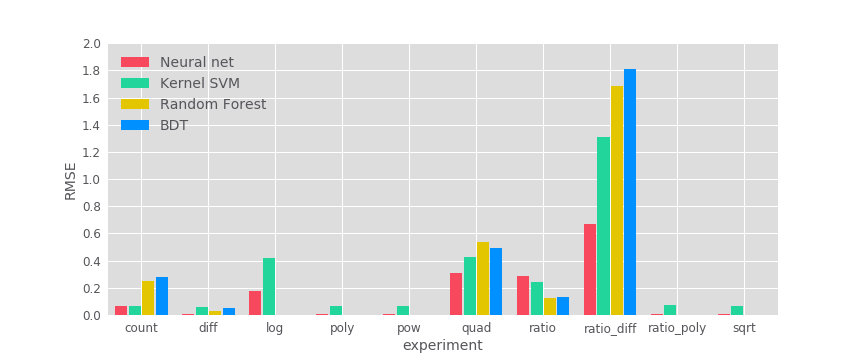
Abbildung 1: Fähigkeit von Machine Learning-Algorithmen zum selbstständigen Erlernen gängiger Feature-Engineering-Methoden. Die Labelwerte lagen einheitlich zwischen 1 und 10. Wäre ein Algorithmus unfähig irgendwelche Muster in den Daten zu modellieren, so würde dieser einen RMSE-Wert von 2,6 erzielen.
In Übereinstimmung mit Heaton’s Analyse ist keiner der Algorithmen in der Lage, Verhältnisse von Differenzen zu erlernen. Darüber hinaus existieren Übereinstimmungen bei den Ergebnissen zu Summen und Verhältnissen. Algorithmen, die auf Decision Trees basieren, performen bei Summen schlechter als andere. Decision Trees haben keine direkte Möglichkeit, mehrere Features zu summieren. Diese müssten für jede mögliche Kombination ein Blatt erstellen, um Summen gut zu erlernen. Neuronale Netze und SVM performen bei Verhältnissen ebenso schlechter. Zudem bestätigen die Ergebnisse wie erwartet, dass Decision Trees monotone Transformationen erlernen können.
Im Gegensatz zu Heatons Analyse zeigt meine Analyse bei quadratischen Distanzen einen deutlichen Unterschied. Alle Modelle haben Probleme beim Erlernen dieses Features. Der Unterschied erklärt sich dadurch, dass in Heaton’s Experiment zu quadratischen Distanzen viele Labels den Wert Null hatten. Die übrigen Werte der Labels waren eher gering.
Die linearen Modelle haben außerdem mehr Probleme, Logarithmen zu erlernen. Die Labels in Heaton’s Experiment zu diesem Feature waren um eine Größenordnung kleiner als in einigen anderen Experimenten. Dadurch lässt sich der Unterschied erklären.
Fazit
Diese Analyse bewertete die Bedeutung von Feature-Engineering-Methoden im Modellierungsprozess. Dies wurde durch Messung der Fähigkeit von Machine Learning-Algorithmen zum selbstständigen Erlernen der Features durchgeführt. Alle getesteten Modelle können einfache Transformationen erlernen. Man kann seine Zeit also effizienter einsetzen, wenn man sich auf Features konzentriert, die auf mehreren anderen Features basieren. Insbesondere wenn diese Divisionen enthalten.
Dies erklärt auch, warum das Kombinieren nicht-verwandter Algorithmen eher zu spürbaren Verbesserungen in der Performance führt als das Kombinieren von ähnlichen Algorithmen. In einem Datensatz mit Mustern, die Summen- und logarithmischen Funktionen ähneln, profitiert beispielsweise das Kombinieren eines BDT und eines Random Forests nur vom Erkennen der logarithmischen Muster. Ein neuronales Netz und ein Random Forest können dagegen von beiden Arten profitieren.
[1] J. Heaton, An Empirical Analysis of Feature Engineering for Predictive Modeling (2016), arXiv
